Muchas gracias por permitir su publicación en español.
Introducción rápida a las redes
neuronales
Este artículo
presenta una introducción a nivel básico del perceptrón multicapa y de la propagación
hacia atrás.
Por Ujjwal Karn
Una red neuronal artificial (RNA) es un modelo informático que
se inspira en la forma en que las redes neuronales biológicas del cerebro
humano procesan la información. Las redes neuronales artificiales han suscitado
mucho entusiasmo en el mundo de la investigación y de la industria del
aprendizaje automático, gracias a los muchos avances conseguidos en el
reconocimiento de voz, la visión por computadora y el procesamiento de textos.
En esta entrada del blog trataremos de llegar a comprender un tipo particular
de red neuronal artificial conocida como perceptrón multicapa.
Una sola neurona
La unidad básica de cálculo en
una red neuronal es la neurona, a menudo llamada nodo o unidad. La neurona
recibe la entrada de otros nodos, o de una fuente externa, y calcula un
resultado que presenta a la salida. Cada entrada tiene un peso asociado (w),
que se asigna en función de su importancia relativa en relación con otras
entradas. El nodo aplica una función f (definida a continuación) a la suma
ponderada de sus entradas como se muestra a continuación en la Figura 1:
Figura 1: neurona
Esta red admite las entradas
numéricas X1 y X2 y tiene los pesos w1 y w2 asociados con esas entradas.
Además, hay otra entrada 1 con
un peso b (conocido como sesgo) asociado a ella. Más adelante
aprenderemos más detalles sobre el papel del sesgo.
La salida Y de la neurona se calcula como se
muestra en la Figura 1. la función f no es lineal y se conoce como
función de activación. El propósito
de la función de activación es introducir la no linealidad en la salida de la
neurona. Esto es importante porque la mayoría de los datos del mundo real no
son lineales y queremos que las neuronas aprendan estas representaciones no
lineales.
Cada función de activación (o de
no linealidad) está representada por un número y realiza una determinada
operación matemática sobre ella [2]. Existen varias funciones de
activación que se pueden encontrar en la práctica:
·
Sigmoide: Se aplica al
número real de una entrada y lo ajusta a un valor entre 0 y 1
·
σ(x) = 1 / (1 + exp(−x))
·
Tangente
hiperbólica: se aplica al número real de una entrada y lo ajusta a un
valor entre [-1, 1]
tanh(x) = 2σ(2x) − 1
·
ReLU: ReLU son las
siglas de Rectified Linear Unit. Se aplica al número real de una entrada y la
ajusta al umbral de cero (sustituye cualquier valor negativos por cero)
·
f(x) = máx (0, x)
Las figuras que aparecen a continuación [2] muestran cada
una de estas funciones de activación.
Figura 2: diferentes funciones de
activación
Importancia del sesgo: El cometido más importante
del sesgo es proporcionar a cada nodo un valor constante entrenable (además de
las entradas normales que el nodo recibe). Ver este
enlace para saber más acerca del
papel del sesgo en una neurona.
Red neuronal unidireccional
La red neuronal unidireccional
fue el primer diseño y el más sencillo de red neuronal artificial [3].
Contiene múltiples neuronas (nodos) dispuestas en capas. Los nodos de las capas
adyacentes tienen conexiones o extremos entre ellos. A todas estas conexiones se les asocian pesos.
En la Figura 3 se muestra un ejemplo de una red neuronal
unidireccional.
Figura 3: ejemplo de red neuronal
unidireccional
Una red neuronal unidireccional puede tener tres tipos de nodos:
1. Nodos de entrada: Los
nodos de entrada proporcionan a la red información del mundo exterior y al
conjunto de los mismos se conoce como 'capa de entrada'. En los nodos de
entrada no se realiza ningún cálculo, se ocupan solo de pasar la información a
los nodos ocultos.
2. Nodos ocultos: Los nodos
ocultos no tienen conexiones directas
con el mundo exterior ( de ahí su denominación de 'ocultos'). Realizan
cálculos y transfieren información de los nodos de entrada a los nodos de
salida. Una colección de nodos ocultos forma una 'capa oculta'. Si bien una red
unidireccional sólo tiene una sola capa de entrada y una única capa de salida,
puede tener varias capas ocultas o incluso ninguna.
3. Nodos de salida: Al conjunto de nodos de salida se le denomina 'capa de
salida' y son los responsables de realizar los cálculos y de la transferencia
de información de la red al exterior.
En una red de unidireccional la
información se mueve en una sola dirección (hacia adelante) desde los nodos de
entrada, a través de los nodos ocultos (si los hay) hacia los nodos de salida.
No hay ciclos o bucles en la red [3] (esta propiedad de
las redes unidireccionales es diferente de la de las redes neuronales
recurrentes, en las que las conexiones entre los nodos forman un ciclo)
A continuación se ofrecen dos ejemplos de redes
unidireccionales:
1. Perceptrón de una sola capa: Esta es
la red neuronal unidireccional más sencilla [4] y
no tiene capas ocultas. Se puede obtener más información sobre perceptrones de
capa única en [4], [5], [6], [7].
2. Perceptrón multicapa: Un
perceptrón multicapa tiene una o más capas ocultas. A continuación estudiaremos
solamente los perceptrones multicapa, ya que son más útiles que los perceptones
de capa única para las aplicaciones prácticas de hoy en día.
Perceptrón multicapa
Un perceptron multicapa (PMC) contiene una o más capas ocultas
(aparte de una capa entrada y una capa de salida). Mientras que un perceptron
de una sola capa sólo puede aprender funciones lineales, un perceptron de
varias capas también puede aprender funciones no lineales.
La figura 4 muestra un perceptrón multicapa con una única capa
oculta. Hay que tener en cuenta que a todas las conexiones se les asocian
pesos, y en la figura se muestran solo tres pesos (w0, w1, w2).
Capa de entrada: La capa de entrada tiene tres
nodos. El nodo de sesgo tiene un valor de 1. Los otros dos nodos toman los
valores X1 y X2 como entradas externas (valores numéricos que dependen de del
conjunto de datos de entrada). Como se ha explicado anteriormente, no se
realiza ningún cálculo en la capa de entrada, por lo que las salidas de los
nodos de la capa de entrada son 1, X1 y X2 respectivamente, los cuales
alimentan a la capa oculta.
Capa Oculta: La capa oculta también tiene tres
nodos, con el nodo de sesgo que proporciona un valor de 1 a la salida. La
salida de los otros dos nodos de la capa oculta depende de las salidas de la
capa de entrada (1, X1, X2) así como de los pesos asociados con las conexiones
(extremos). La figura 4 muestra el cálculo de salida para uno de los nodos
ocultos (resaltado). Del mismo modo, se puede calcular el valor de la salida
del otro nodo oculto. Recuerde que f se refiere a la función de activación.
Estas salidas alimentan a los nodos de la capa de salida.
Figura 4: perceptron multicapa
con una capa oculta
Capa de salida: La capa de salida tiene dos nodos
cuyas entradas proceden de la capa oculta y realizan cálculos similares, como
se muestra en el caso del nodo oculto resaltado. Los valores obtenidos (Y1 e
Y2) como resultado de estos cálculos son las salidas del perceptrón multicapa.
Dado un conjunto de
características X = (x1, x2, ...) y
un objetivo y, un perceptrón
multicapa puede aprender la relación entre las características y el objetivo,
ya sea tanto para operaciones de clasificación como de regresión.
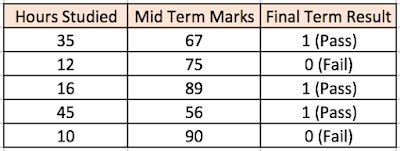
Veamos un ejemplo para entender mejor los perceptrones
multicapa. Supongamos que tenemos el siguiente conjunto de calificaciones de
estudiantes:
Las dos columnas de entrada muestran el número de horas de
estudio y el valor medio de las calificaciones obtenidas por el estudiante. La
columna 'Resultado final' puede tener dos valores 1 o 0 que indican si el
estudiante pasó el examen final. Por ejemplo, podemos ver que si el estudiante
estudió 35 horas y obtuvo una nota media de 67, terminó pasando el examen
final.
Ahora, supongamos, queremos predecir si un estudiante que
estudia 25 horas y que tiene una nota media de 70 pasará el examen final.
Este es un problema de clasificación binaria en el que un
perceptron de varias capas puede aprender de los ejemplos dados (datos de
entrenamiento) y hacer una predicción con criterio sobre nuevos datos. Veremos
a continuación cómo un perceptrón multicapa aprende tales relaciones.
Entrenamiento del PMC: El Algoritmo de propagación hacia atrás
Al proceso por el cual un
perceptrón multicapa aprende se le llama algoritmo de propagación hacia atrás. Recomendaría
la lectura de esta respuesta en Quora
de Hemanth Kumar (citada a
continuación) que explica la propagación hacia atrás de forma muy clara.
La propagación hacia atrás de errores, abreviada
a menudo como BackProp es una más de las diferentes formas con las que se puede
entrenar una red neuronal artificial (RNA). Es un programa de entrenamiento
supervisado, lo que significa que aprende de los datos de entrenamiento
etiquetados (hay un supervisor para guiar su aprendizaje).
Para expresarlo en términos
simples, BackProp es como 'aprender de los errores'. El supervisor corrige la
RNA cuando comete errores.
Una RNA consta de nodos dispuestos en diferentes capas; la capa
de entrada, la(s) capa(s) oculta(s) intermedia(s) y la capa de salida. A las
conexiones entre nodos de capas adyacentes se les asocian 'pesos'. El objetivo
del aprendizaje es asignar pesos correctos a estas conexiones o extremos. Dado
un vector de entrada, estos pesos determinan cuál es el vector de salida.
En el aprendizaje supervisado, el conjunto de entrenamiento está
etiquetado. Esto significa que, para algunas entradas dadas, podemos conocer la
salida deseada / esperada (etiqueta).
Algoritmo BackProp:
Inicialmente todos los pesos de
las conexiones se asignan al azar. La RNA se activa para cada entrada del
conjunto de datos de entrenamiento, y se observa su salida. Esta salida se
compara con la salida deseada que ya conocemos, y el error se 'propaga' hacia
atrás, a la capa anterior. Este error se anota y los pesos se 'ajustan' en
consecuencia. Este proceso se repite hasta que el error de salida está por
debajo de un umbral predeterminado.
Cuando el citado algoritmo ha concluido su ejecución, tenemos
una RNA 'que ha aprendido' y que consideramos que está preparada para trabajar
con 'nuevas' entradas. Se dice que esta RNA ha aprendido de varios ejemplos
(datos etiquetados) y de sus errores (propagación de errores).
Ahora que tenemos una idea de cómo funciona la propagación hacia
atrás, volvamos a nuestro conjunto de notas de los estudiantes mostrado antes.
El perceptrón multicapa que se
muestra en la figura 5 (adaptado de la excelente explicación visual del algoritmo de propagación hacia
atrás de Sebastian Raschka) tiene dos
nodos en la capa de entrada (aparte del nodo de sesgo) que recoge las entradas
'horas estudiadas' y 'nota media'. También tiene una capa oculta con dos nodos
(aparte del nodo de sesgo). La capa de salida tiene dos nodos también, el nodo
superior da salida a la probabilidad de 'aprobado' mientras que el nodo
inferior genera la probabilidad de 'suspenso'.
En tareas de clasificación,
utilizamos generalmente una función Softmax como
función de activación en la capa de salida
del perceptrón multicapa para asegurar que las salidas son
probabilidades y suman 1. La función Softmax toma un vector de puntuaciones
arbitrarias de valores reales y lo ajusta a un vector de valores entre cero y
uno y suman uno. Así pues, en este caso,
Probabilidad (aprobado) + Probabilidad (suspenso)
= 1
Paso 1: Propagación hacia adelante
Todos los pesos de la red se
asignan al azar. Consideremos a continuación el nodo de la capa oculta marcado
con una V en la Figura 5. Supongamos que los pesos de las conexiones de las
entradas a ese nodo son w1, w2 y w3 (como se muestra en la figura).
La red toma entonces el primer ejemplo de entrenamiento como
entrada (sabemos que para las entradas 35 y 67, la probabilidad de aprobar es
1).
·
Entrada a la red = [35, 67]
·
Salida deseada de la red (objetivo) = [1, 0]
·
Entonces la salida V del nodo que
estamos considerando se puede calcular como vemos a continuación (f es una
función de activación tal como la sigmoide):
V = f (1*w1
+ 35*w2 + 67*w3)
Del mismo modo se calculan también las salidas del otro nodo en
la capa oculta. Las salidas de los dos
nodos en la capa oculta constituyen las entradas a los dos nodos en la capa de
salida. Esto nos permite calcular las probabilidades de salida de los dos nodos
en la capa de salida.
Supongamos que las probabilidades de salida de los dos nodos en
la capa de salida son 0,4 y 0,6 respectivamente (ya que los pesos se asignan al
azar, las salidas también serán aleatorias). Podemos ver que las probabilidades
calculadas (0,4 y 0,6) están muy lejos de las probabilidades deseadas (1 y 0,
respectivamente), por lo que la red en la Figura 5 se dice que tiene una
'salida Incorrecta'.
Figura 5: paso de propagación
hacia adelante en un perceptrón multicapa
Paso 2: Propagación hacia atrás y actualización de los pesos
Calculamos el error total en los
nodos de salida y propagamos estos errores de nuevo a través de la red usando
la propagación hacia atrás para calcular los gradientes. Luego utilizamos un
método de optimización como el descenso adaptativo para 'ajustar' todos los
pesos en la red con el objetivo de reducir el error en la capa de salida. Esto
se muestra en la Figura 6 a continuación (por ahora se pueden ignorar las
ecuaciones matemáticas que aparecen en la figura).
Suponga que los nuevos pesos asociados con el nodo en
consideración son w4, w5 y w6 (después de la propagación hacia atrás y de los
pesos de ajuste).
Figura 6: paso de propagación hacia atrás y
actualización de pesos en un perceptrón
multicapa
Si ahora aplicamos a la red el mismo ejemplo, la red debería
funcionar mejor que antes, ya que los pesos se han ajustado para minimizar el
error en la predicción. Como se muestra en la Figura 7, los errores en los
nodos de salida ahora se reducen a [0,2, -0,2] en comparación con [0,6, -0,4]
anterior. Esto significa que nuestra red ha aprendido a clasificar
correctamente nuestro primer ejemplo de entrenamiento.
Figura 7: la red PMC funciona ahora mejor con
la misma entrada
Repetimos este proceso con todos
los demás ejemplos de entrenamiento de nuestro conjunto de datos. Entonces,
podemos decir que nuestra red ha aprendido esos ejemplos.
Si ahora queremos predecir si un estudiante que estudia 25 horas
y tiene una nota media de 70 puntos pasará el examen final, ejecutaremos el
paso de propagación hacia adelante y encontraremos las probabilidades de salida
para los resultados de aprobado y suspenso.
He evitado utilizar aquí las
ecuaciones matemáticas y la explicación de conceptos tales como 'descenso
adaptativo' y he intentado desarrollar una explicación intuitiva para el
algoritmo. Para aprender de un análisis
en el que se utilizan las matemáticas del algoritmo de propagación hacia atrás,
se puede consultar este enlace.
Visualización 3d de un perceptrón multicapa
Adam Harley ha creado una visualización
en 3d de un perceptrón multicapa
que ya ha sido entrenado (utilizando la propagación hacia atrás) sobre la base
de datos MNIST de dígitos escritos a mano.
La red toma 784 valores de
píxeles numéricos como entradas de una imagen 28 x 28 de un dígito escrito a
mano (tiene 784 nodos en la capa de entrada correspondientes al mismo número de
píxeles). La red tiene 300 nodos en la primera capa oculta, 100 nodos en la
segunda capa oculta, y 10 nodos en la capa de salida (correspondiente a los 10
dígitos) [15].[15].
Aunque la red descrita aquí es mucho más grande (usa más capas y
nodos ocultos) en comparación con la que discutimos en la sección anterior,
todos los cálculos en el paso de propagación hacia adelante y el paso de
propagación hacia atrás se hacen de la misma manera (en cada nodo) como se comentó
antes.
La Figura 8 muestra la red cuando la entrada es el dígito '5'.
Figura 8: visualización de la red para una
entrada de '5'
Un nodo que tiene un valor de salida más alto que otros nodos
está representado por un color más brillante. En la capa de entrada, los nodos
brillantes son aquellos que reciben entradas de valores de píxeles numéricos
más altos. Observe cómo en la capa de salida, el único nodo brillante
corresponde al dígito 5 (tiene una probabilidad de salida de 1, que es mayor
que los otros nueve nodos que tienen una probabilidad de salida de 0). Esto
indica que el PMC ha clasificado correctamente el dígito de entrada. Recomiendo
jugar con esta visualización y observar las conexiones entre nodos de
diferentes capas.
Redes neuronales profundas
Conclusión
Con el objetivo de facilitar la
comprensión del tema, he omitido detalles importantes de algunos de los
conceptos discutidos en esta entrada. Para profundizar en el conocimiento de
los perceptrones multicapa, recomendaría estudiar las Parte1, Parte2, Parte3 y el Estudio del Caso del
tutorial sobre redes neuronales de Stanford.
Si tiene alguna pregunta o sugerencia, por favor ¡escríbala en
los comentarios a continuación!
Biografía: Ujjwal
Karn tiene una experiencia de 3
años sobre aprendizaje automático en los campos de la industria y la
investigación y está muy interesado en las aplicaciones prácticas de
aprendizaje profundo a la comprensión de los procesos del lenguaje y de la
visión.
Referencias
15. A. W. Harley, "An Interactive Node-Link
Visualization of Convolutional Neural Networks," in ISVC, pages 867-877,
2015 (enlace)